I have been working on building a chess engine and a key part of evaluating a chess position involves assigning values to individual chess pieces.
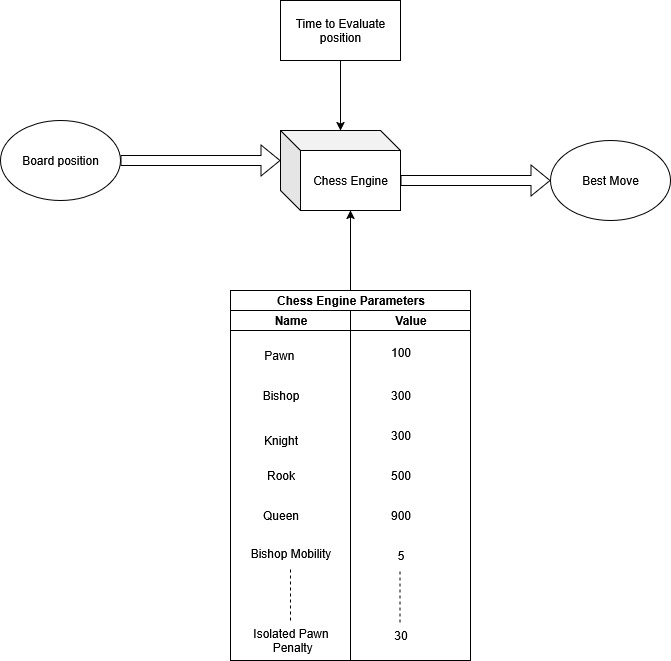
For reference: this is the architecture of my chess engine (along with most conventional chess engines). The engine needs to evaluate a chess position and assign it a score, for that we need to pass the values of different chess pieces and other parameters used in your chess engine.
One of the first rules taught to beginners learning chess is that chess pieces follow the following ratio:
Queen ≈ 9 Pawns
Rook ≈ 5 Pawns
Bishop ≈ 3 Pawns
Knight ≈ 3 Pawns
But, But, But, how do we know that this ratio is correct? Or if these are the most optimal ratios, then how can we prove that!
Also, my chess engine uses many other parameters like:
1. Piece mobility of all pieces
2. Doubled pawn, isolated pawns and passed pawns
3. King Safety & Center control
Our task ahead is cut out for us and I want to find the optimal value of all these parameters.
Genetic Algorithms
The core idea of evolution is that organisms with favorable traits for that environment are more likely to survive and pass those traits to future generations.
A single chromosome can be defined as a combination of values for all the chess engine parameters.
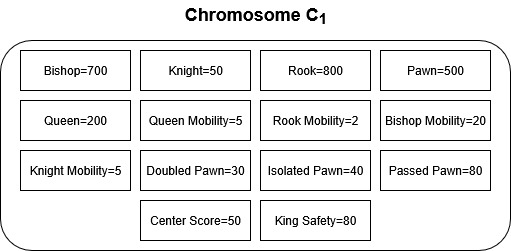
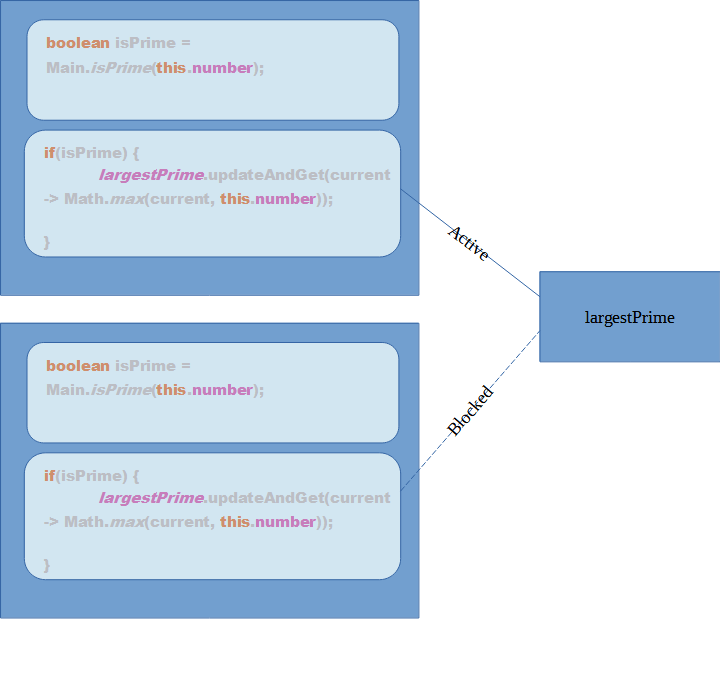
We will initialize a population with N chromosomes. Now, we will make each Chromosome play with each other. So, C1 chromosome will play (N-1) games with other chromosomes and C2 chromosome will play (N-2) games with other chromosomes and so on.
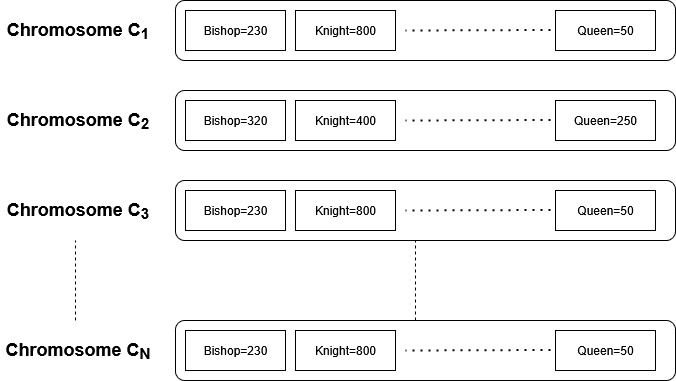
So, in total there will be N*(N-1)/2 games in total.
For each match between 2 chromosomes, we will assign a score of 1 for the winner and -1 for the loser and 0 if the game was a draw. After all combinations of matches have been played, we will have a ranking table as follows:

Now, we will keep top S chromosomes and discard the rest N-S chromosomes for the next iteration. We have done a “selection” of S chromosomes that are relatively stronger and will do a crossover operation among them to generate a set of N-S chromosomes so that we have a set of N chromosomes for the next iteration.
How do we do mutation of chromosomes to generate a new chromosome? – the simplest way is to select two chromosomes C1 and C2 and do a selection as follows:
Cmix (Bishop) = Random(0,1) > 0.5 ? C1 (Bishop) : C2(Bishop)
To ensure that our population maintains diversity and doesn’t overfit, we will follow a process of mutation.
Cmix (Bishop) = Random(0,1) < MUTATION_RATIO ? Random(0,1000) : Cmix(Bishop)
Results
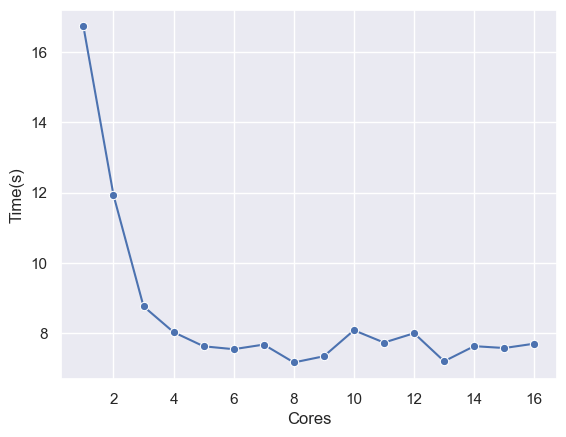
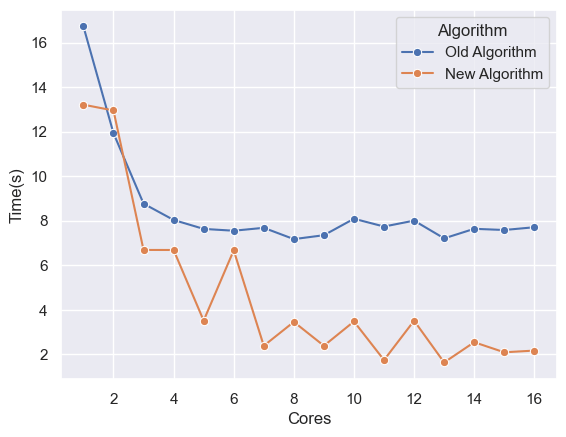
I ran this experiment for N=10 population, S=4 (top 4 chromosomes preserved in each iteration), MUTATION_RATIO=25. For all games, I gave the engine 2 seconds to think of the best move.
This experiment was run on a 8-core virtual server so that 8 games can be played simultaneously and each iteration would take ~1.5 hours for 45 games played. After 2-3 days of running this simulation, I got the following results
Iteration 1:
ITERATION 41:

| Piece | Iteration 0 | Iteration 20 | Iteration 40 |
| Pawn | 50 | 50 | 50 |
| Rook | 40 | 170 | 580 |
| Knight | 140 | 360 | 290 |
| Bishop | 360 | 440 | 390 |
| Queen | 640 | 440 | 930 |
| Bishop Mobility | 8 | 7 | 7 |
| Rook Mobility | 3 | 6 | 0 |
| Knight Mobility | 6 | 6 | 6 |
| Queen Mobility | 0 | 6 | 6 |
| Doubled Pawn Penalty | 2 | 9 | 6 |
| Isolated Pawn Penalty | 1 | 6 | 1 |
| Passed Pawn Bonus | 2 | 9 | 6 |
| King Safety | 2 | 9 | 6 |
| Center Control | 7 | 9 | 2 |
We can clearly observe that by iteration 40, our piece values converged to their conventional values. Interesting observation is that bishops are given more value than knights.
The key observation is that we produced these results without any prior knowledge or biases related to chess as part of our parameter tuning mechanism by just using Genetic Algorithms!