games – Parv Maurya

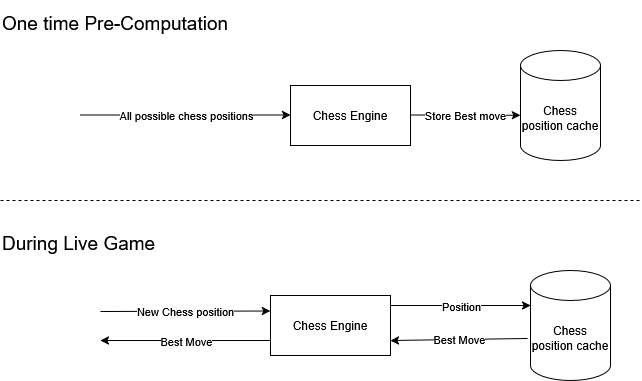
In the last article we understood the basics of a chess engine. In this article we will explore the most fundamental computation in a chess engines – to evaluate how good or bad a position is and how do I do it in my Foresight engine. We want to be able to attribute a score to every chess position, so that we can find the best move by maximizing the score if it’s White’s move to play or minimize the score if it’s Black’s move to play.

Why does a good evaluation function matter?

By design, our engine will prefer to reach positions as per our evaluation function – eg: if our engine values bishops more than knights then we would try to reach a position where we have more bishops and less knights relative to your opponent.

Another critical use of a good eval function – alpha beta pruning in minimax which is the core of all conventional chess engines work well i.e effectively prune a large number of nodes only when we are able to distinguish between as many types of positions. But we will explore move tree generation and alpha beta pruning at a later time.

What should be the chess position evaluation function as written in the rules of the game?

Simply assign +1 value to position where the white king checkmates black king and -1 for vice versa. For all other positions you can assign a score of 0.

But, but, there is a catch – Practically most positions don’t lead to checkmate and you don’t have enough computing power in the world to compute the route to checkmate in a “quiet” position.

Conventional wisdom of hundreds of years of humans playing chess states that having more pieces generally leads to checkmating the opponent king. Think of it this way – would you rather have more pieces or less than your opponent when starting the game??

Obviously this a gross simplification of the game – since you can checkmate the king even after sacrificing a few pieces to do so.

We will use this assumption to do some feature engineering and

Let’s imagine a simple evaluation function:

function EVALUATION-SIMPLE(board):
    score <- 0
    
    score <- score + board.getTotalWhitePawns() * 100
    score <- score + board.getTotalWhiteBishops() * 300
    score <- score + board.getTotalWhiteKnights() * 300
    score <- score + board.getTotalWhiteRooks() * 500
    score <- score + board.getTotalWhiteQueen() * 900

    score <- score - board.getTotalBlackPawns() * 100
    score <- score - board.getTotalBlackBishops() * 300
    score <- score - board.getTotalBlackKnights() * 300
    score <- score - board.getTotalBlackRooks() * 500
    score <- score - board.getTotalBlackQueen() * 900

    return score

EVALUATION-SIMPLE() is a simple function which assigns static value to individual pieces on the board. These values are generally used by humans when playing chess, bishops and knights are 3 times as valuable as a pawn, rook is considered 5 times as valuable as a pawn and a queen is considered the most valuable piece with a value of 9 times a pawn.

Consider the following position, our simple evaluation function will give the score as follows: (5 pawns * 100 + 2 bishops * 300 + 2 knights * 300 + 2 rooks * 500 + 1 queen * 900 ) – (7 pawns * 100 + 2 bishops * 300 + 2 bishops * 300 + 2 rooks * 500 + 1 queen * 900) = -200

This means that our simple evaluation function prefers this position for Black and believes that Black is doing well in this position.

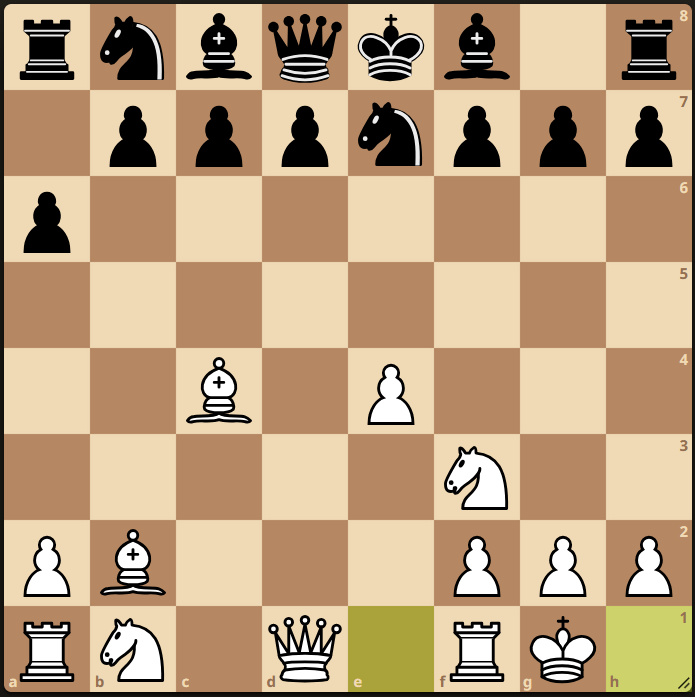
But as we can see in the image above, the white bishops are very powerful and mobile in the long open diagonals, the white king is safe in the corner, white knight on f3 is also well placed. Whereas black pieces are immobile, with no central control, blocked bishops and king still in the center – the black king is primed for an attack by the white pieces.

So even though black is better as per our simple evaluation we know that it is white who is playing for a Win in this position.

This means that we need additional features to be part of our evaluation function like king safety, piece mobility, pawn structure.

Piece Mobility

A knight is a more mobile and active piece in the middle of the board, a bishop is a more active piece when it has open diagonals. A rook becomes more menacing when it stares down open files. In short, active and mobile pieces enhance their quality, mobile pieces enable your position to create attacks on the opposite king or win some of the enemy pieces.

For the purpose of defining a simple mobility metric:
MOBILITY_SCORE(PIECE) = Number of legal moves PIECE can make.

But how do we find the number of legal moves a piece can make, more importantly, how do we do it FAST

To do that we will detour a bit and delve into BITBOARDS.

BITBOARDS:

Bit operations are fundamental operations understood by any CPU (AND, OR, XOR, Left Shift, Right Shift etc) which makes them extremely fast.

Observe, 1101 = 1 * 2³ + 1 * 2² + 0 * 2¹ + 1 * 2⁰ = 13
Here, 13 can used to represent an ordering. It can be an ordering of 4 chairs where 1 means the chair is occupied and 0 means that its empty.
If you want to find the total number of empty chairs, the program would look something like this:

while (number > 0) {
        if number & 1
                count++
        number >>1
}

This is many many times faster than if you represented the chairs as a list of Chair object where each Chair object can have a state of empty or occupied. Your program will internally have to assign memory whenever the Chair object is created and your Garbage Collector in Java will have to release that memory after some time. So if you are planning to do such operations millions of times in a second, then you will need to utilize the bitwise representation.

Now, lets see how we can transfer this knowledge into Chess. We will first flatten the 2D chessboard into a 1D 64 bit number as follows:
And of course 1<<x = 2^x

Now, we will define such 8×8 layers represented by a 64 bit number for 6 types of white pieces (pawn, rook, bishop, knight, queen, king) and 6 types of black pieces. Which means any chess position can be represented by 12 64-bit numbers.

Now, lets say we need to create a layer which contains all the white pieces:


WHITE-PIECES-LAYER = WHITE-KING-LAYER | WHITE-BISHOP-LAYER | 
                     WHITE-KNIGHT-LAYER | WHITE-ROOK-LAYER |
                     WHITE-PAWN-LAYER | WHITE-QUEEN-LAYER

Where | is the bitwise OR operator

Lets generalize how, this flattened representation of a chessboard can be used to traverse the chess board.

Now, that we have some idea about the ease and utility of using bitboards to represent piece wise layers, lets use bitwise operations to find the mobility of the bishop.

In this position, the bishop is situated at 1<<18 position, Bishops can only move diagonally, so our algorithm to find the mobility of the bishop should be such that we keep moving in all four diagonals and add to our mobility count till we are blocked by any piece. And if the blocked piece is the enemy piece, we will add 1 to the mobility count and break the loop since capturing the enemy piece is also a legal move. We will also break the loop if we reach the end of board.

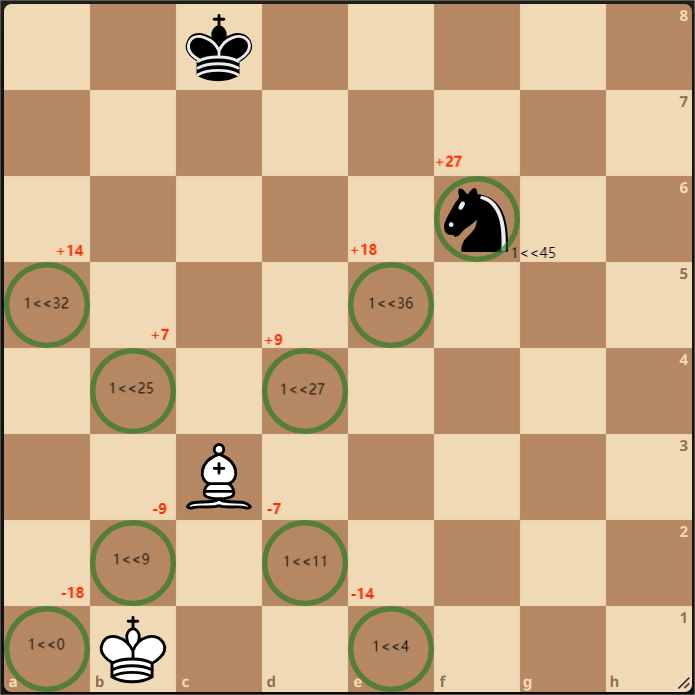
Algorithm for the above stated mechanism:

WHITE-BISHOP-MOBILITY-SCORE(bishop_layer):
  bishop_offset = [-7, -9, 7, 9]
  mobility = 0
  
  while bishop_layer > 0:
    bishop_layer = bishop_layer & (bishop_layer - 1)
    bishop_position = CountTrailingZeros(bishop_layer)

    for ( offset: bishop_offset ):
      multiplier = 1
      while  0<= bishop_position + multiplier * offset <64:

        if not IsEndOfBoard(bishop_position + multiplier*offset):
          if bishop_position & (whitePieces | blackPieces) == 0:
            mobility++
          elif bishop_position & (whitePieces | blackPieces) != 0:
            mobility++
            break
          else:
            break

    return mobility

You can design similar function for Rook, Queen and Knight mobility with some modifications. You should also look out to pre-compute anything which is repeatedly being evaluated.

Position evaluation time

I will show how long my engine takes to evaluate a single chess position, I will profile it by running the function millions of times.

I ran the position evaluation of a complex chess position 10 million times and here are the results:

	Static Evaluation	Static Evaluation + Piece Mobility	Static Evaluation + Piece Moblility + Pawn Structure + King Safety
Total Time	8.8 ms	1768.4 ms	3609.6 ms
Time per position	0.9 ns	176.8 ns	361.0 ns

As we can see evaluating a position is blazing fast. My evaluation time per position at one time was ~2000 ns which was becoming a bottleneck for my engine.
After some profiling I could see that I was creating an object everytime my position evaluation function got called, since object creation is an expensive operation – you need to allocate a memory for that object and also causes Garbage Collector Backpressure related issues when millions of objects are created.
This object creation itself was taking an average of ~1400-1600 ns. I optimized my program such that I no longer require a new object creation everytime.
I also did a lot of pre-compute which sped-up the mobility calculator function.

You might be thinking that if it takes 361 ns to evaluate a single position, I should be able to evaluate 1e9/361 = 2.77 million positions per second. But in practice I am able to evaluate 0.2-0.5 million positions per second. This is because my program currently has a lot of overhead (A lot of it should be resolved by removing unnecessary object allocation).

Why Build This Chess Engine?

I’ve been fascinated by chess since I started playing around seven years ago. This is actually my third try at building a chess engine. The first two fizzled out, but this time, I committed more seriously and finally saw meaningful progress. The name of this engine is Foresight and this is the first part in a series of articles articulating my journey.

The best way to learn is by doing. You think you understand something as simple as how to sort a list of numbers until you actually implement a high-performance sorting algorithm and compare it to state-of-the-art solutions. You then realize there are CPU-level optimizations, cache-aware designs, and memory access patterns that you wouldn’t discover without hands-on exploration.

Similarly, I had recently read an excellent book on Java concurrency, and I wanted to apply that knowledge in a domain I had decent familiarity with: chess engines.

Initially, I thought it would be cool to parallelize the alpha-beta minimax algorithm and enjoy performance gains. It turns out, though, that alpha-beta pruning is a peculiar algorithm. Beyond a point, parallelism yields diminishing returns and, paradoxically, can slow down the engine, depending on the number of cores and the specific parallel strategy employed.

How Does a Chess Engine Work?

At its core, a chess engine evaluates a board and decides the best move. Chess has a 8×8 grid board with a fixed starting position. Each player has the same number of pawns ♙, rooks ♖, bishops ♗, knights ♘, queen ♕ when the game starts. Each of these piece move uniquely and the goal of the game is to checkmate the enemy King. Alternately the game can end in a draw due to insufficient material or Fifty-move_rule.

Unlike games like Poker that involve hidden information, chess is a game of complete information. Both players see the entire board.

The primary goal in chess is simple: checkmate the opponent’s king. While checkmates can sometimes be forced with a known sequence of moves, most positions in real games are too complex for such deterministic conclusions.

Is Chess already solved?

On the surface Chess is like Tic-Tac-Toe : both are a 2D complete information, turn based, zero-sum games. Even a human can become perfect in Tic-Tac-Toe in less than a day i.e always playing the best move in given position. We all know Chess Engine computers are extremely strong now. So, do we already have a database where we have stored the best moves for all possible positions. Above statement has been visualized as follows:

Tic-Tac-Toe has only 765 unique positions, so it’s feasible to store the best move for every scenario. In contrast, chess explodes in complexity.

After just six moves from the opening position, there are over 10^7 unique positions. Storing them all would need at least 1.4 GB memory (assuming 140 bytes per board state), and that’s just scratching the surface.
The total number of distinct chess positions is estimated to be over 10^45.

Chess is not a solved game like Tic-Tac-Toe. Solved as in we have not pre-computed all possible positions. We will also learn that it’s practically impossible to find the best move for most chess positions and have to always settle for an approximation.

So brute-force pre-computation is off the table. Instead, engines dynamically evaluate each board state and the above architecture is not possible in practice.

Chess Algorithm

If Chess is a computable problem, then we should be capable of writing an algorithm to find the best move, given a chess position, we will make all possible moves and will find the move where we get the best score, here is the algorithm:

function FIND-BEST-MOVE(board, isWhite):
    bestMove ← null

    if isWhite then:
        bestScore ← −∞
    else:
        bestScore ← ∞

    for each move ∈ ALL-LEGAL-MOVES(board) do:
        MAKE-MOVE(board, move)
        score ← FIND-SCORE(board, ¬isWhite)
        UNDO-MOVE(board, move)

        if score > bestScore and isWhite then:
            bestScore ← score
            bestMove ← move
      
        if score < bestScore and not isWhite then:
            bestScore <- score
            bestMove <- move

    return bestMove

White will try to find a position with the maximum score leading to the checkmate of the black king and therefore avoid the move leading to the checkmate of the white king and vice-versa.

Now, all we need to do is to define the FIND-SCORE function, since we know that there is only one objective in chess – to checkmate the opponent’s king. Score is 1 when white king is checkmated, -1 when black king is checkmated and 0 in case of a draw position. Possible states of a board: {0, 1, -1}.

function FIND-SCORE(board, isWhite):
    if WHITE-CHECKMATED(board): return −1
    if BLACK-CHECKMATED(board): return 1
    if DRAW(board): return 0

    if isWhite then:
        bestScore ← −∞
    else:
        bestScore ← ∞

    for each move ∈ ALL-LEGAL-MOVES(board) do:
        MAKE-MOVE(board, move)
        score ← FIND-SCORE(board, ¬isWhite)
        UNDO-MOVE(board, move)

        if isWhite then:
            bestScore ← max(bestScore, score)
        else:
            bestScore ← min(bestScore, score)

    return bestScore

There is nothing wrong with this algorithm, except that when you run this algorithm: you are basically trying to find the move which leads to checkmate and this recursive algorithm in practice will take an impractical time to execute since chess positions are rarely instantly leading to checkmate in X moves. Also lets assume that the checkmate takes 40 moves to reach, this algorithm will need to evaluate an ungodly number of positions (35⁴⁰ positions considering an average branching factor of 35) and will take years in practice to evaluate that checkmate.

Assume F(board, side) is a computable algorithm for a chess engine, here’s what we can do to improve the above algorithm is make few assumptions based on practical chess play:

The FIND-SCORE() algorithm practically can’t be infinitely recursive, we would like cutoff this evaluation this evaluation at a certain depth and it is a reasonable assumption that looking at X moves ahead will lead to better evaluation than looking at Y moves ahead if X>Y.

FIND-SCORE(depth = 10) >> FIND-SCORE(depth=5)
Any chess player knows that much before checkmates come to picture, a player will try to capture as many pieces of the opponent as possible while losing as little of your own pieces. Also practical chess playing shows that certain pieces are more valuable than others like queen is more valuable than a rook and a bishop is more valuable than a pawn.

We will create another function FIND-SCORE-STATIC-EVALUATION(), which also considers the individual pieces on the board, and other custom features like mobility of pieces which humans have observed

So, if the position is not a checkmate, we want to use all the pieces on the board to find a net score with the assumption that having more pieces on the board will eventually lead to checkmating the enemy king. tldr: having more pieces on the board compared to the opponent has a high correlation to checkmating the enemy king.

FIND-SCORE() ≈ FIND-SCORE-STATIC-EVALUATION()

In the upcoming articles we will delve into how to design the FIND-SCORE-STATIC-EVALUATION() using techniques like bitboard representation, bitwise operations and using alpha-beta pruning among other techniques to efficiently prune the move tree.

Tag: games

Foresight: How to evaluate a chess position?

What should be the chess position evaluation function as written in the rules of the game?