Lets get started
The purpose of this article is to use multithreading in Java to compute the largest prime number less than 1e7. We will observe some interesting things as we go along.
How do we know if a number is prime?
We will use an intuitive and a good enough primality check algorithm.
This algorithm has a O(√n) time complexity where n is the number to be tested. There are faster algorithms to test primality, we can explore them in future but are beyond the scope of this article.
static boolean isPrime(long number) {
for(int i=2; i<Math.ceil(Math.sqrt(number)); ++i) {
if(number%i == 0) {
return false;
}
}
return true;
}How do we find the largest prime number less than 1e8.
public static void sequentialPrimeCalculation(){
long maxPrime = -1;
long startTime = System.currentTimeMillis();
for(long i=2; i<1e7; ++i){
if (isPrime(i)) {
maxPrime = Math.max(i, maxPrime);
}
}
System.out.println("Largest prime is: " + maxPrime);
System.out.println("Computation took: " + (System.currentTimeMillis()- startTime)/1000.0 + " ms");
}Output:
Largest prime is: 9999991
Computation took: 15.036 ms
We now have a baseline for a sequential/single threaded code.
Lets start with multithreading now
We can see that each individual primality test in the sequential code is independent. This makes it a suitable task to be parallelized.
Each individual task will do the primality test and store it in a AtomicLong variable which is thread-safe and hence can be accessed safely within each task.
static AtomicLong largestPrime = new AtomicLong(2);static class PrimeTask implements Runnable {
long number;
PrimeTask(long n) {
this.number = n;
}
@Override
public void run() {
boolean isPrime = Main.isPrime(this.number);
if(isPrime) {
largestPrime.updateAndGet(current -> Math.max(current, this.number));
}
}
}We will use a thread pool, where each threadpool internally maintains a queue of tasks to be submitted are pushed.
If the threadpool finds an idle/free core, it will pop a task from the queue and utilize that core. Once the task is finished, the core is available for other tasks in the threadpool.
public static void parallelPrimeCalculation(int numberOfThreads){
final ExecutorService exec = Executors.newFixedThreadPool(numberOfThreads);
long startTime = System.currentTimeMillis();
for(long i=2; i<1e7; ++i){
exec.submit(new PrimeTask(i));
}
try {
exec.shutdown();
exec.awaitTermination(100, TimeUnit.SECONDS);
} catch (InterruptedException e) {
throw new RuntimeException(e);
}
System.out.println("Number of threads: " + numberOfThreads);
System.out.println("Largest prime is: " + largestPrime.get());
System.out.println("Computation took: " + (System.currentTimeMillis()- startTime)/1000.0 + " ms");
}Output:
Number of threads: 2
Largest prime is: 9999991
Computation took: 11.282 ms
The execution time is better than before, although it is not twice as fast as the sequential code.
Lets plot the time taken for prime computation with thread count:
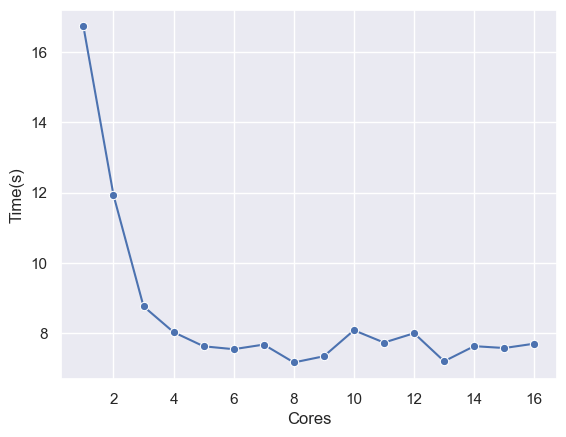
The above plot is a classical case of diminishing returns where the computation time plateaued after 6 cores.
To understand why this happened, we need to revisit our previous assumption that each of our tasks are independent of each other. Because if all our tasks are completely independent, we should observe a linear reduction in computation time as we increase the number of cores and not a plateau.
We can divide a single instance of PrimeTask in two parts: Block 1 and Block 2

We can see that Block 2 of the PrimeTask is accessing a global AtomicLong variable with a blocking operation. As visible below, Block 2 of both the threads try to access the largestPrime number, but it can be accessed only one at a time, which means the other thread will have to wait, which makes our program a bit sequential in such cases.
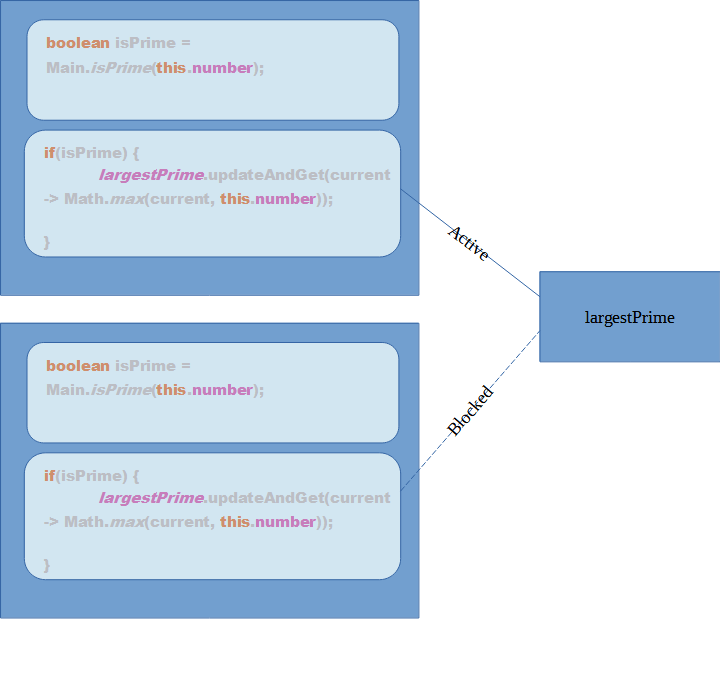
We can improve our Algorithm by eliminating the Block 2 of our PrimeTask.
We will divide the search space [2, 1e7] between all the threads and each thread will store the largest prime that thread has encountered till then. Once all the threads have completed their execution, we will combine the results of all individual threads and get the maximum prime number.
We have redesigned the PrimeTask as follows:
static class PrimePoolTask implements Callable<Long> {
long start;
long offset;
long end;
PrimePoolTask(long start ,long offset, long end) {
this.start = start;
this.offset = offset;
this.end = end;
}
@Override
public Long call() {
long maxNum = -1;
for(long i=start; i<end; i+=offset){
boolean isPrime = Main.isPrime(i);
if(isPrime) {
maxNum = Math.max(i, maxNum);
}
}
return maxNum;
}
}We will now divide the search space and call the PrimePoolTask to find the largest prime number:
public static void parallelPrimeImprovedCalculation(int numberOfThreads){
final ExecutorService exec = Executors.newFixedThreadPool(numberOfThreads);
long startTime = System.currentTimeMillis();
List<Future> maxPrimePerThread = new ArrayList<>();
for(int i=1; i<=numberOfThreads; ++i){
PrimePoolTask task = new PrimePoolTask(i, numberOfThreads, (long) 1e7);
Future<Long> future = exec.submit(task);
maxPrimePerThread.add(future);
}
long maximumPrime = -1;
for(Future<Long> future: maxPrimePerThread){
try {
maximumPrime = Math.max(maximumPrime, future.get());
} catch (InterruptedException | ExecutionException e) {
throw new RuntimeException(e);
}
}
System.out.println("Number of threads: " + numberOfThreads);
System.out.println("Largest prime is: " + maximumPrime);
System.out.println("Computation took: " + (System.currentTimeMillis()- startTime)/1000.0 + " ms");
compTime.add((System.currentTimeMillis()- startTime)/1000.0);
}Lets look at the results of this modified algorithm and how it compares with the old algorithm.
We can see that it is much faster, although it also plateaus. In a perfect world if a single core program takes ~16 seconds, then a 16 core program should take ~1 second. But we converged at ~2 seconds.
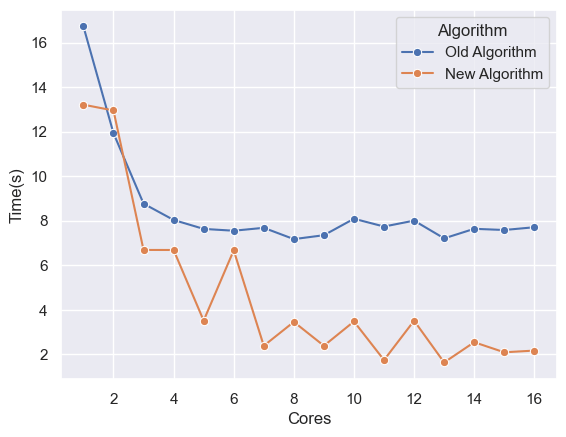
There are several overheads when we do multi-threading which can lead to performance degradation.
For now we can close this discussion and one day we can deep dive into further optimizing this algorithm.
Hope this was informative.
Note: Of course the fastest way to do that is to not do a primality check from 1-> 1e8 but 1e8->1, but the purpose of the article to demonstrate multi-threading in java and not on the semantics of the problem. 🙂
